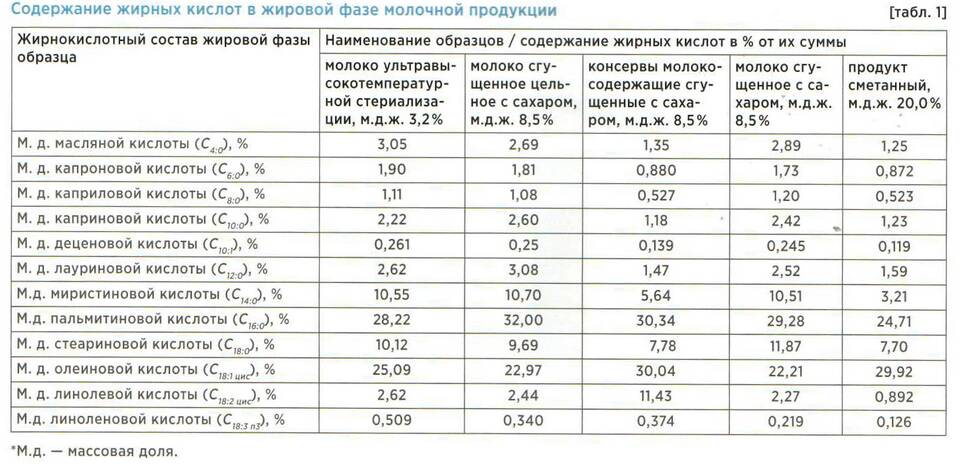
В математическом анализе и алгебре понятие суммы играет фундаментальную роль. Рассмотрим ключевые выводы о свойствах и значении суммы в различных разделах математики.
Содержание
В математическом анализе и алгебре понятие суммы играет фундаментальную роль. Рассмотрим ключевые выводы о свойствах и значении суммы в различных разделах математики.
Основные выводы о свойствах суммы
- Сумма является базовой арифметической операцией
- Подчиняется фундаментальным законам математики
- Имеет широкое применение в различных областях знаний
Математические выводы
| Свойство | Вывод |
| Коммутативность | Порядок слагаемых не влияет на результат |
| Ассоциативность | Группировка слагаемых не меняет сумму |
| Дистрибутивность | Сумма распределяется относительно умножения |
Выводы о применении суммы
- В алгебре: основа для построения более сложных операций
- В анализе: база для определения интеграла
- В теории вероятностей: основа для расчетов ожиданий
- В информатике: фундамент алгоритмов
Философские выводы
- Сумма представляет собой синтез частей в целое
- Демонстрирует принцип аддитивности в природе
- Является мерой совокупного воздействия
Практические выводы
| Область | Значение суммы |
| Экономика | Баланс доходов и расходов |
| Физика | Результирующая сила |
| Инженерия | Суммарная нагрузка |
Таким образом, понятие суммы не ограничивается простой арифметической операцией, а представляет собой глубокую математическую концепцию с широкими приложениями в науке и практике.
