Доверительный интервал - это статистический показатель, который определяет диапазон значений, с заданной вероятностью содержащий истинный параметр генеральной совокупности. Рассмотрим его сущность, методы расчета и область применения.
Содержание
Основные характеристики доверительного интервала
| Параметр | Описание |
| Уровень доверия | Вероятность (обычно 90%, 95% или 99%), что интервал содержит истинное значение |
| Границы интервала | Нижняя и верхняя оценка возможных значений параметра |
| Ширина интервала | Зависит от объема выборки и изменчивости данных |
Формула расчета доверительного интервала
Для среднего значения (нормальное распределение)
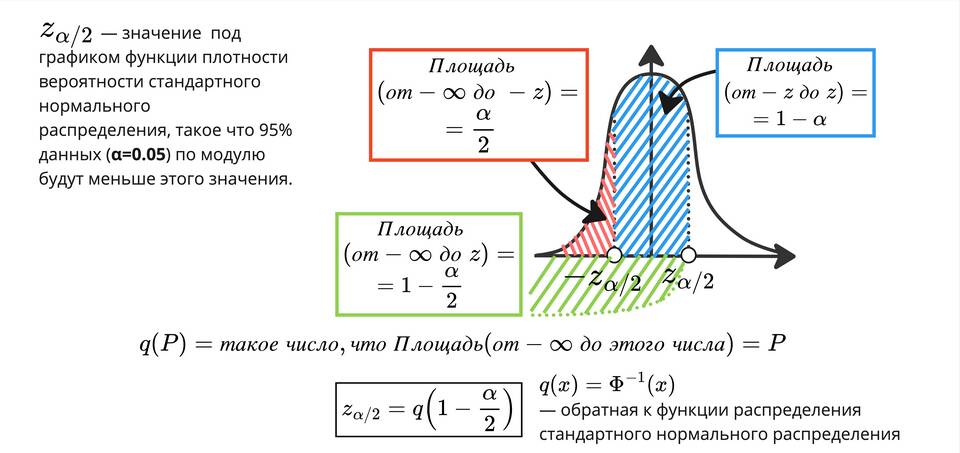
ДИ = x̄ ± z*(σ/√n)
- x̄ - выборочное среднее
- z - критическое значение z-распределения
- σ - стандартное отклонение
- n - объем выборки
Для пропорции (биномиальное распределение)
ДИ = p̂ ± z*√(p̂(1-p̂)/n)
- p̂ - выборочная пропорция
- z - критическое значение
- n - объем выборки
Факторы, влияющие на доверительный интервал
| Фактор | Влияние на интервал |
| Объем выборки | Увеличение n уменьшает ширину интервала |
| Уровень доверия | Рост уровня доверия увеличивает интервал |
| Изменчивость данных | Большая вариация расширяет интервал |
Примеры применения доверительных интервалов
В научных исследованиях
- Оценка эффективности лекарств
- Анализ социологических опросов
- Экспериментальные исследования в психологии
В бизнес-аналитике
- Прогнозирование продаж
- Оценка доли рынка
- Анализ удовлетворенности клиентов
Интерпретация доверительных интервалов
| Ситуация | Правильная интерпретация |
| ДИ для разницы средних включает ноль | Нет статистически значимой разницы |
| ДИ полностью выше/ниже контрольного значения | Статистически значимый эффект |
| Широкий ДИ | Недостаточный объем данных или высокая вариабельность |
Распространенные ошибки
- Путаница с вероятностью нахождения параметра в интервале
- Интерпретация 95% ДИ как области, содержащей 95% данных
- Игнорирование при сравнении групп
Доверительный интервал является мощным инструментом статистического вывода, позволяющим оценить точность измерений и надежность результатов. Правильное понимание и применение ДИ помогает избежать ошибочных выводов в исследованиях и анализе данных.