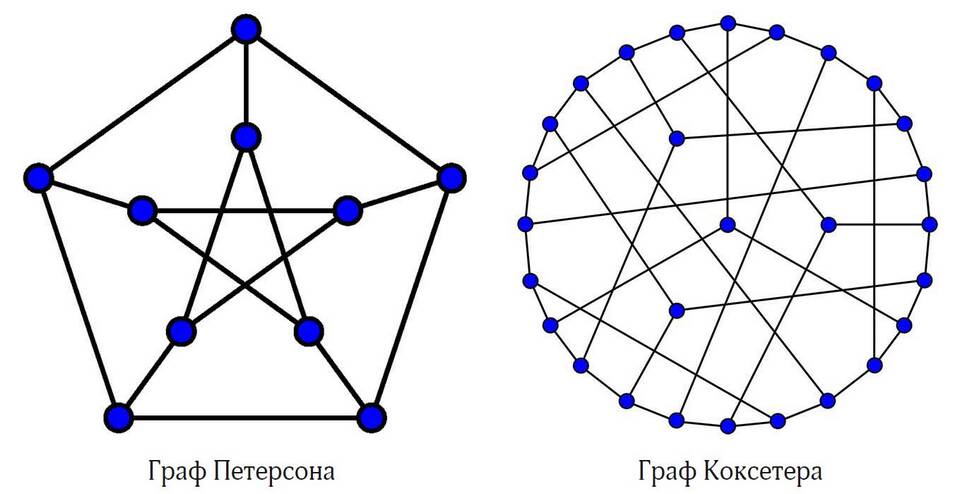
В теории графов существует фундаментальная теорема, утверждающая, что сумма степеней всех вершин графа равна удвоенному количеству его ребер. Приведем строгое доказательство этого утверждения.
Содержание
В теории графов существует фундаментальная теорема, утверждающая, что сумма степеней всех вершин графа равна удвоенному количеству его ребер. Приведем строгое доказательство этого утверждения.
Формулировка теоремы
Для любого неориентированного графа G = (V, E) без петель и кратных ребер выполняется равенство:
| ∑ deg(v) = 2|E| |
| где v ∈ V, deg(v) - степень вершины, |E| - количество ребер |
Основные понятия
- Степень вершины - количество ребер, инцидентных данной вершине
- Ребро - неупорядоченная пара вершин
- Граф - совокупность вершин и соединяющих их ребер
Доказательство теоремы
Метод двойного подсчета
- Рассмотрим произвольный граф G с n вершинами и m ребрами
- Каждое ребро соединяет ровно две вершины
- При подсчете суммы степеней каждое ребро учитывается дважды:
- Один раз для первой вершины ребра
- Один раз для второй вершины ребра
- Следовательно, общая сумма степеней всех вершин равна удвоенному количеству ребер
Формальное доказательство
| Шаг | Обоснование |
| 1. Пусть граф имеет m ребер | По условию теоремы |
| 2. Каждое ребро вносит вклад +1 в степень каждой из двух вершин | Определение инцидентности |
| 3. Общий вклад одного ребра в сумму степеней равен 2 | 1 + 1 = 2 |
| 4. Для m ребер общая сумма степеней равна 2m | m × 2 = 2m |
Следствия из теоремы
1. Лемма о рукопожатиях
В любом графе количество вершин с нечетной степенью всегда четно.
2. Оценка количества ребер
Для графа с n вершинами максимальное количество ребер составляет:
- n(n-1)/2 для полного графа
- n-1 для дерева
Пример применения
| Граф | Степени вершин | Сумма степеней | Количество ребер |
| Треугольник | 2, 2, 2 | 6 | 3 |
| Звезда с 4 лучами | 4, 1, 1, 1, 1 | 8 | 4 |
Применение в теории графов
Доказанная теорема используется при:
- Анализе сетевых структур
- Построении алгоритмов обхода графов
- Доказательстве других теорем теории графов
- Решении задач комбинаторики
Представленное доказательство показывает фундаментальную связь между локальными характеристиками вершин и глобальными свойствами графа, подтверждая строгую математическую закономерность.
